부울 대수는 아리스토텔레스의 유명한 삼단논법을 수학적으로 분석할 수 있는 방법론을 제공합니다. 이 고대의 논리 구조 중 첫 두 전제를 다시 검토해 보겠습니다:
- 모든 인간은 죽는다.
- 소크라테스는 인간이다.
여기서 '인간'을 P, '죽음'을 M, 그리고 '소크라테스'를 S로 표현해 보겠습니다. "모든 인간은 죽는다"는 주장은 사실상 인간이 죽음을 포함하는 집합, 즉 인간과 죽음의 교집합이 모든 인간을 포함한다는 것을 의미합니다.

모든 죽는 존재에는 인간 외에도 고양이, 개, 심지어 나무까지 포함될 수 있기 때문에, P AND M = M이라는 명제는 성립하지 않습니다. "소크라테스는 인간이다"라는 말은 소크라테스를 포함하는 집합이 인간이라는 더 큰 집합과 겹친다는 것, 즉 소크라테스가 인간 집합에 포함된다는 것을 나타냅니다.
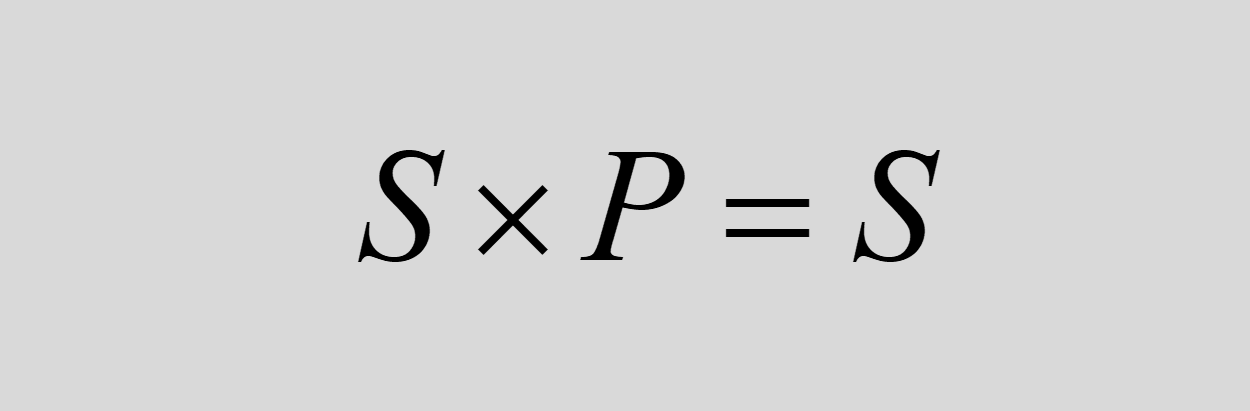
첫 번째 전제에서 인간이 죽음을 포함한다는 것(P x M = P)을 알게 되었으므로, 두 번째 전제는 다음과 같이 표현될 수 있습니다.

결합 법칙을 적용하면, 다음과 같은 식이 도출됩니다: (S x P) x M = S
여기서 (S x P)가 S임을 알고 있으므로, 이를 대입하여 단순화하면 다음과 같이 표현할 수 있습니다.

결과적으로, 이 식은 소크라테스가 죽음의 집합에 포함되어 있음을 나타내며, 따라서 소크라테스가 죽을 것이라는 결론을 내립니다. 만약 (S x M)의 결과가 0이라면, 소크라테스가 죽지 않는다는 결론을 내릴 수 있으며, 결과가 M이라면, 모든 것이 불멸이지만 소크라테스만이 죽는 유일한 존재라는 결론에 이를 수 있습니다.
부울 대수로 2400년 전 소크라테스가 자명하게 증명한 사실을 다시 증명하는 것이 다소 과잉처럼 느껴질 수 있습니다. 그럼에도 불구하고, 부울 대수는 특정 조건을 만족하는지를 판별하는 데 유용하게 쓰일 수 있습니다. 상상해 보세요, 어느 날 당신이 애완동물 가게를 방문하여 점원에게 이런 요청을 한다고 합시다:
"중성화된 수컷이면서 하얀색 또는 황갈색인 고양이를 원해요. 또는 중성화된 암컷인데 하얀색이 아닌 고양이도 좋아요. 그리고 검정색 고양이라면 성별이나 중성화 여부와 상관없이 모두 좋습니다." 이때, 점원이 "그러면 당신이 찾는 고양이는 다음 수식으로 표현될 수 있습니다. 이게 맞나요?"라고 묻는다면, 당신은 "네, 맞습니다"라고 답할 수 있습니다.

점원의 제안이 정확한지 확인하기 위해, '합집합'과 '교집합'이라는 용어 대신 'OR'과 'AND'라는 용어를 사용하는 것이 좋을 것 같습니다. 이 단어들을 대문자로 표기한 이유는, 이들이 단순한 영어 단어를 넘어 부울 대수에서의 특정 연산을 지칭하기 때문입니다. 어떤 요소가 '첫 번째 집합' OR '두 번째 집합'에 속한다면, 그 요소는 두 집합 중 하나 이상에 포함된다는 것을 의미합니다. 반면, 어떤 요소가 '첫 번째 집합' AND '두 번째 집합'에 동시에 속한다면, 그 요소는 두 집합 모두에 포함되어 있다는 것을 나타냅니다. 여기서 'NOT'이라는 용어는 특정 집합에서 요소를 제외하는 연산을 나타내기 위해 사용됩니다. 요약하면, - 합집합을 나타내던 + 기호는 이제 OR로 해석됩니다.
- 교집합을 나타내던 × 기호는 이제 AND로 해석됩니다.
- 전체 집합에서 특정 요소를 제외하는 1- 연산은 이제 NOT로 해석됩니다.
이를 바탕으로, 앞서의 수식은 다음과 같이 변환할 수 있습니다:

이제 우리가 필요로 하는 설명을 대부분 마쳤습니다. 아래 수식을 통해 애완동물 가게에서 원하던 고양이 유형을 괄호 사용으로 명확히 표현한 방법을 살펴봅시다. 당신이 찾던 고양이는 다음 세 가지 유형 중 하나였습니다.

이 수식을 바탕으로 판매원은 불 대수를 활용한 검증 작업, 즉 불 검사를 수행할 수 있습니다. 부울 대수를 사용하는 이 방식은 앞서 설명된 내용과 약간 다른 점이 있으나, 아직 구체적으로 언급하지 않았습니다. 이 부울 대수 방식에서, 문자는 더 이상 단순히 범주를 나타내지 않습니다. 대신, 문자에는 값으로 0 또는 1만이 할당될 수 있습니다. 여기서 1은 긍정적이거나 참인 상태를, 조건을 만족하는 고양이를 의미하며, 0은 부정적이거나 거짓인 상태를, 즉 조건을 만족하지 않는 고양이를 의미합니다.
'IT 기초' 카테고리의 다른 글
| 스위치를 이용한 컴퓨터 논리의 구현 (0) | 2024.02.21 |
|---|---|
| 0과 1, 컴퓨터의 논리(4) (0) | 2024.02.20 |
| 0과 1, 컴퓨터의 논리(2) (0) | 2024.02.16 |
| 0과 1, 컴퓨터의 논리(1) (1) | 2024.02.15 |
| 2진수, 컴퓨터가 세상을 이해하는 방법 (0) | 2024.02.14 |



