이제 우리는 조지 부울의 대수적 원리를 전자 회로에 적용하여 이진 로직을 기반으로 하는 컴퓨터 설계와 구성을 탐구할 실험에 착수할 시점입니다. 첫 번째 실험으로, 전구와 배터리를 평소와 같이 연결하되, 한 개가 아닌 두 개의 스위치를 사용해 볼 것입니다. 이 두 스위치는 하나는 왼쪽에, 다른 하나는 오른쪽에 위치하도록 직렬 연결합니다.

이렇게 직렬로 연결된 스위치 구성에서는, 한쪽 스위치만 닫혀도 전구에 불이 들어오지 않습니다. 같은 방식으로, 한쪽 스위치가 열린 상태에서 다른 한쪽을 닫아도 아무런 변화가 없습니다.

전구가 켜지려면, 아래 그림과 같이 왼쪽 '그리고(and)' 오른쪽 스위치 둘 다가 닫혀 있어야 합니다.

여기서 핵심은 '그리고(and)'라는 용어입니다. 전류가 흐르기 위해서는 왼쪽 '그리고' 오른쪽 스위치 둘 다 닫혀 있어야 합니다. 이러한 회로는 논리적 연산의 기본을 보여주며, 실제로 전구는 "두 스위치가 모두 닫혀 있습니까?"라는 질문에 대한 답이 됩니다. 이 회로의 작동 원리는 다음과 같은 표로 요약할 수 있습니다.
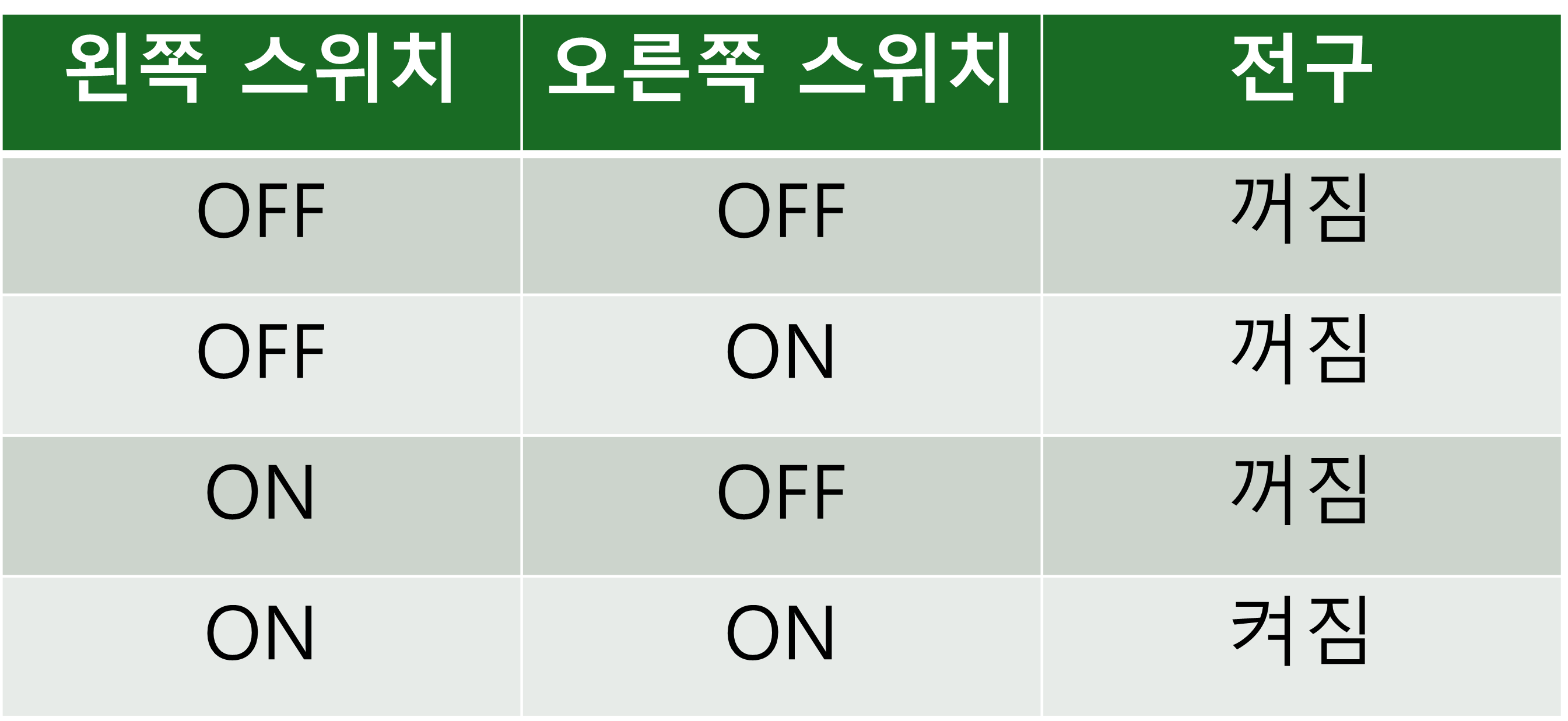
이전 글에서 모든 것을 비트, 즉 이진수로 표현할 수 있다는 사실을 확인했습니다. 비트 값 0으로 '평가자의 엄지손가락이 아래를 향함'을, 비트 값 1로 '엄지손가락이 위를 향함'을 나타낼 수 있었습니다. 스위치의 두 상태 역시 비트로 표현할 수 있으며, 여기서 0은 '스위치가 off', 1은 '스위치가 on'을 의미합니다. 전구의 두 상태 역시 한 비트로 나타낼 수 있으며, '전구가 꺼짐'은 0으로, '전구가 켜짐'은 1로 표현할 수 있습니다. 이제, 위의 설명을 기반으로 표를 간단하게 다시 작성할 수 있습니다.
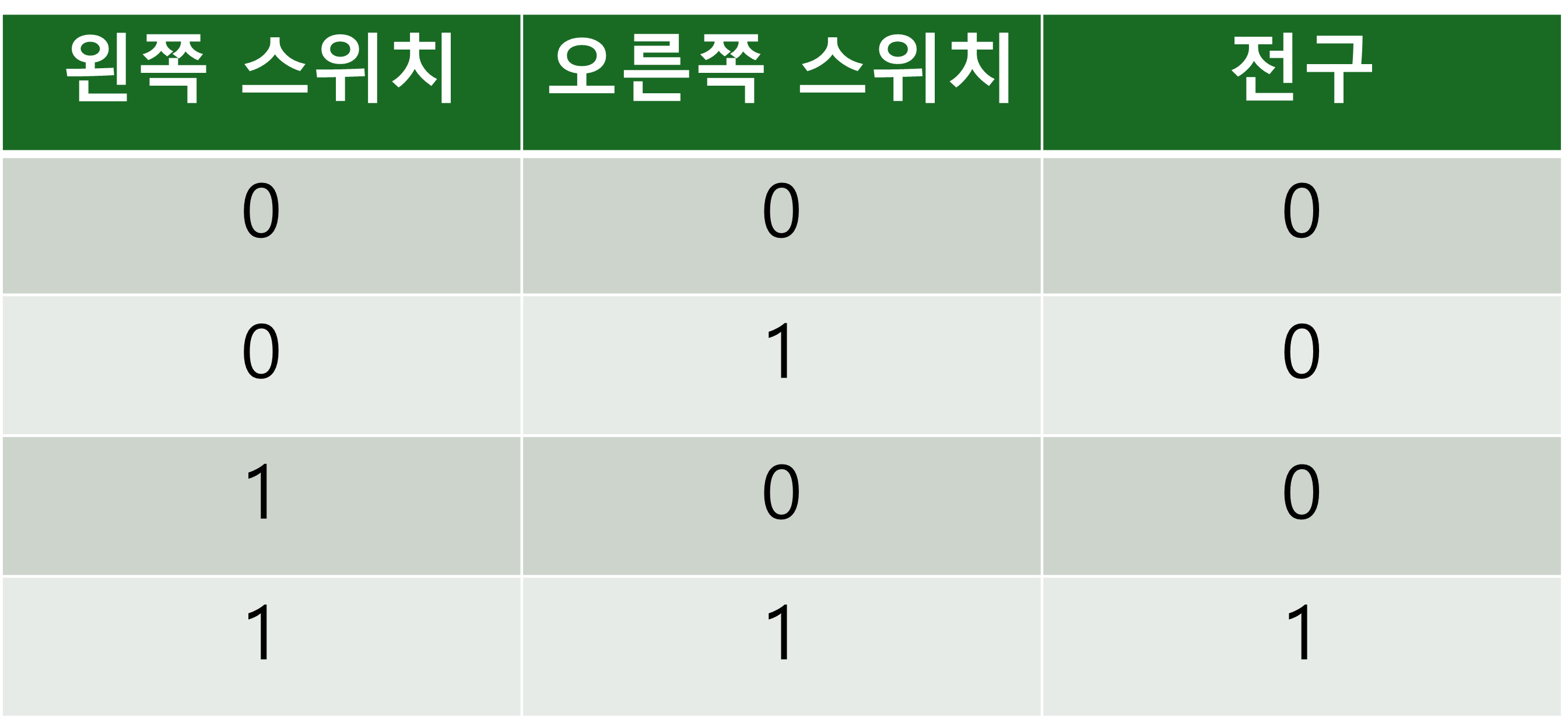
스위치의 위치가 바뀌어도 결과에 영향을 주지 않음을 주목해야 합니다. 즉, 스위치의 위치에 구애받지 않는다는 의미입니다. 그러므로, 이 표는 앞서 소개된 AND 및 OR 연산 표와 유사한 방식으로 다시 작성될 수 있습니다.

결과적으로, 이 간단한 회로를 통해 부울 대수의 AND 연산을 시각적으로 확인할 수 있었습니다.
이제 병렬로 연결된 두 스위치의 구성을 살펴보겠습니다.
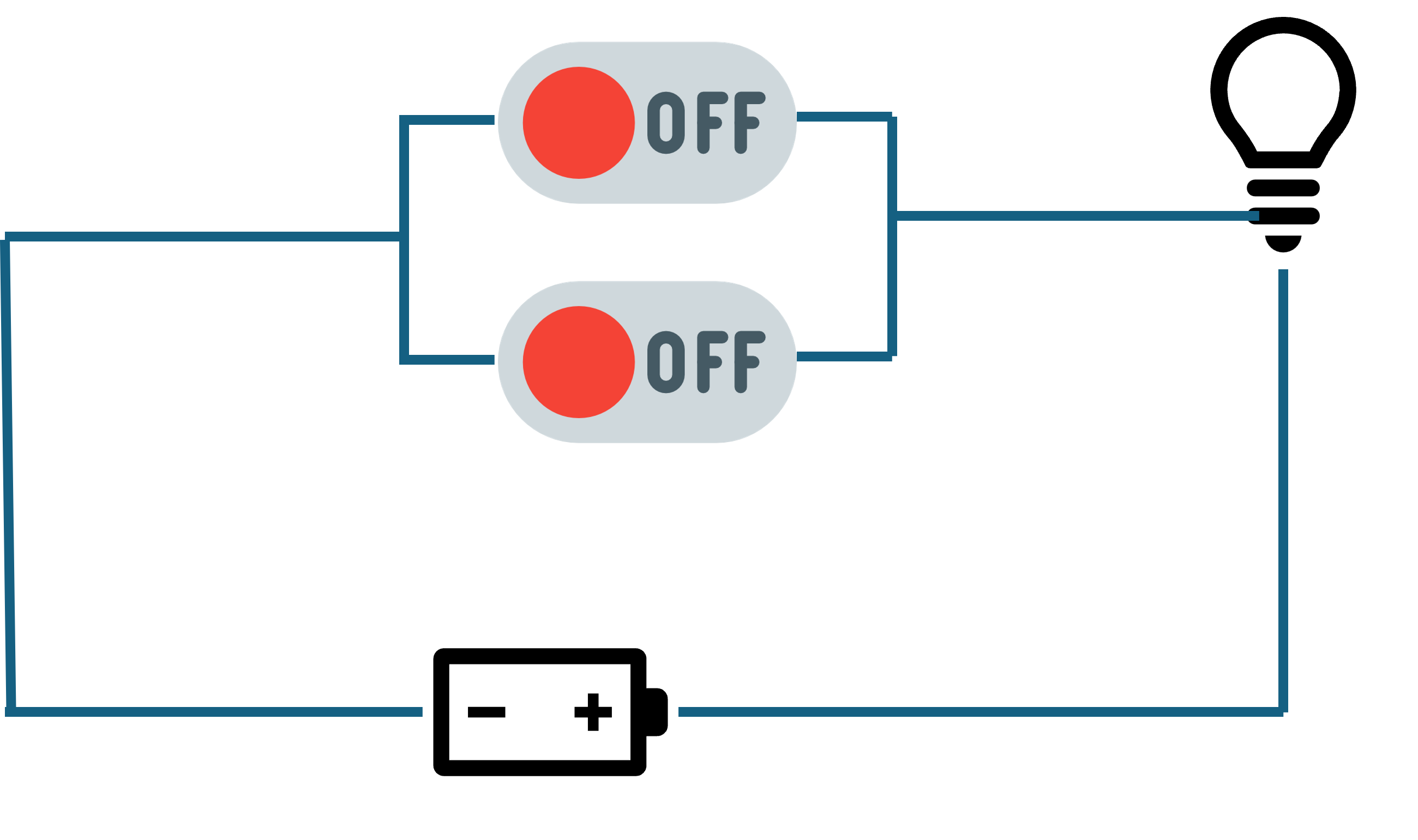
이런 설정에서는 스위치들이 병렬 연결되어 있습니다. 이 구성의 특징은 상단 스위치를 닫으면 전구가 켜진다는 점입니다.

하단 스위치를 닫거나 둘 다 닫으면 역시 전구에 빛이 나옵니다.
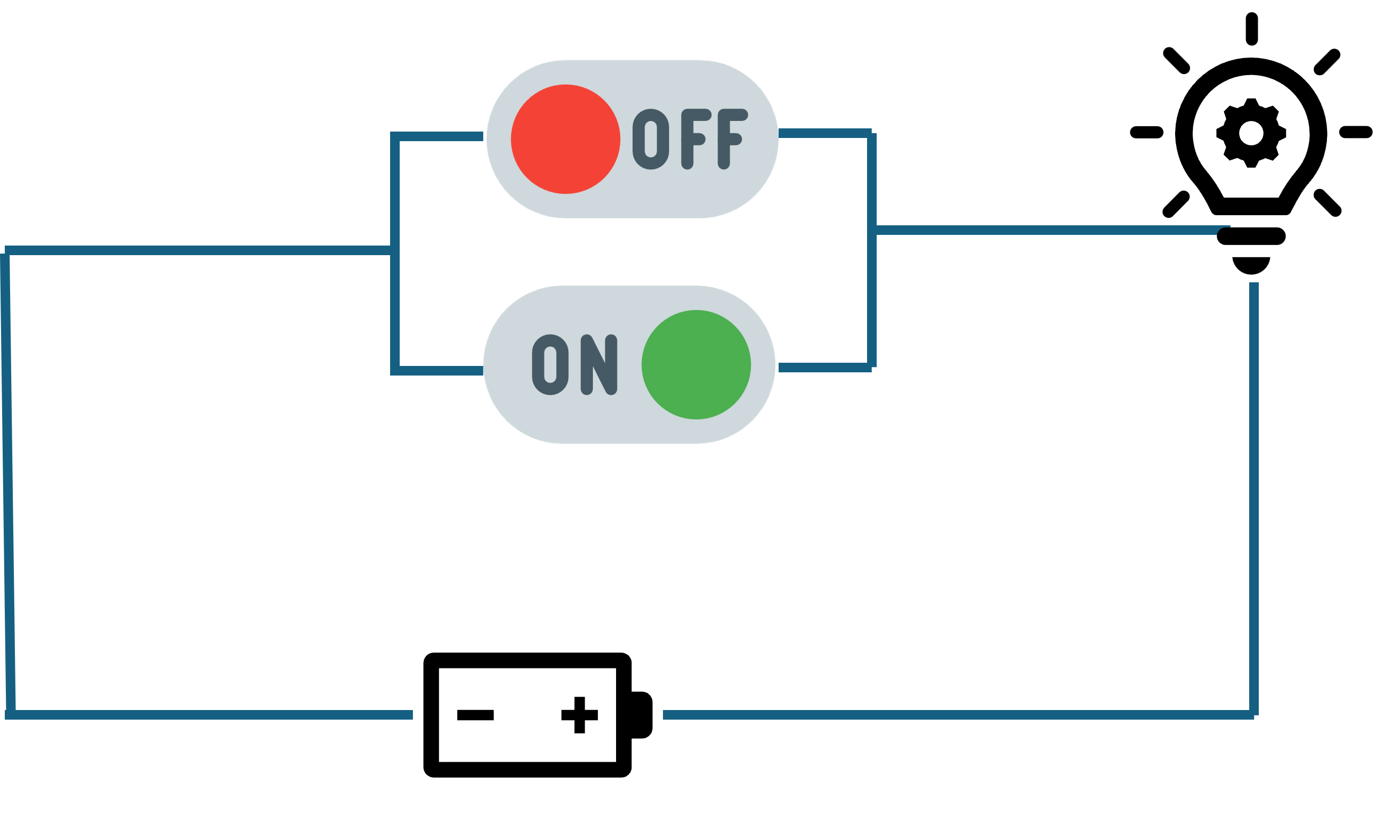
즉, 상단 스위치 '또는(or)' 하단 스위치 중 하나만 닫혀 있어도 전구에 빛이 난다는 의미입니다. 여기서 주요한 용어는 '또는(or)'입니다. 이 설계는 "어느 한 스위치라도 닫혀 있습니까?"라는 질문에 대한 답을 논리적으로 나타냅니다. 이 회로의 작동 방식을 요약한 표는 다음과 같습니다.
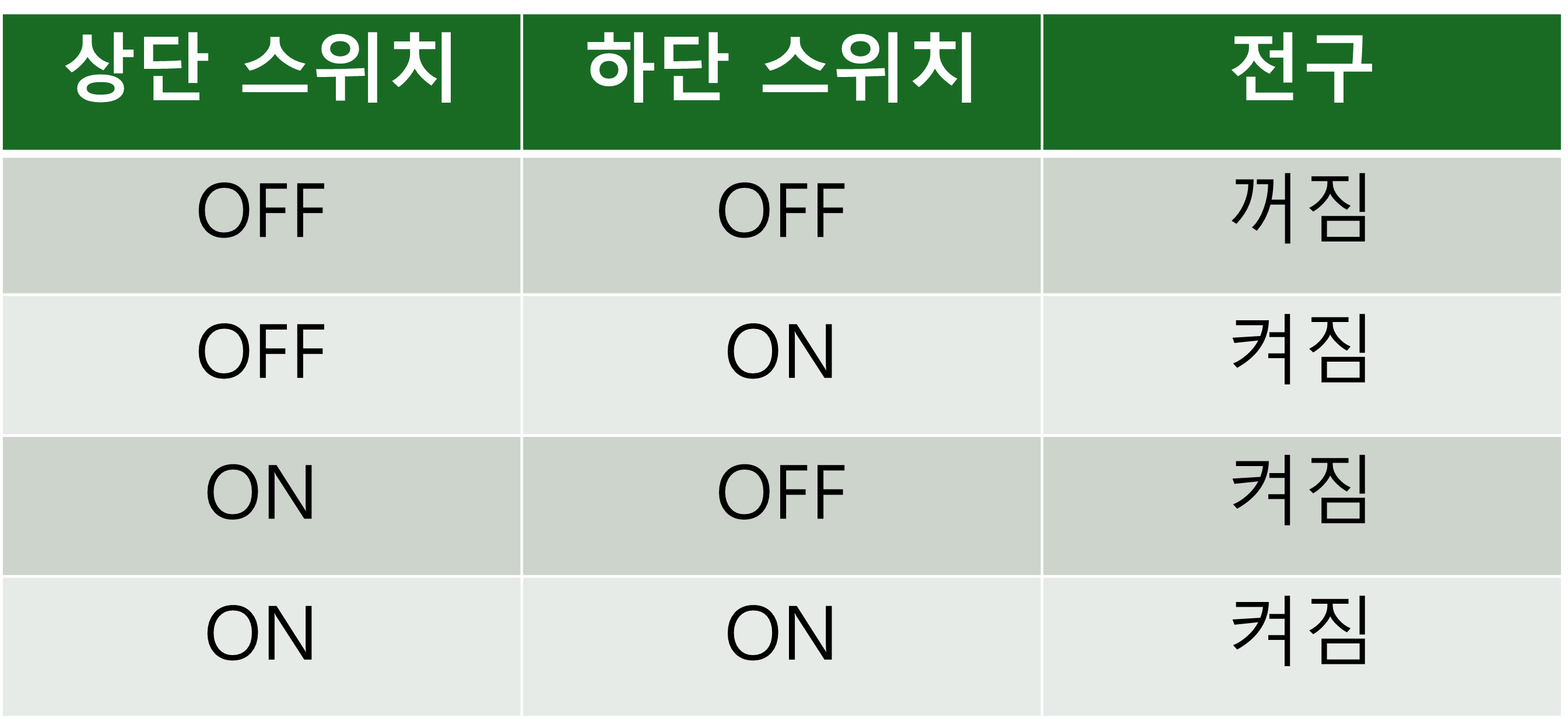
앞서 0은 '스위치 off' 또는 '전구가 꺼짐'을, 1은 '스위치가 on' 또는 '전구가 켜짐'을 나타낸다고 했습니다. 그러므로, 위의 표는 다음과 같이 표현될 수 있습니다.
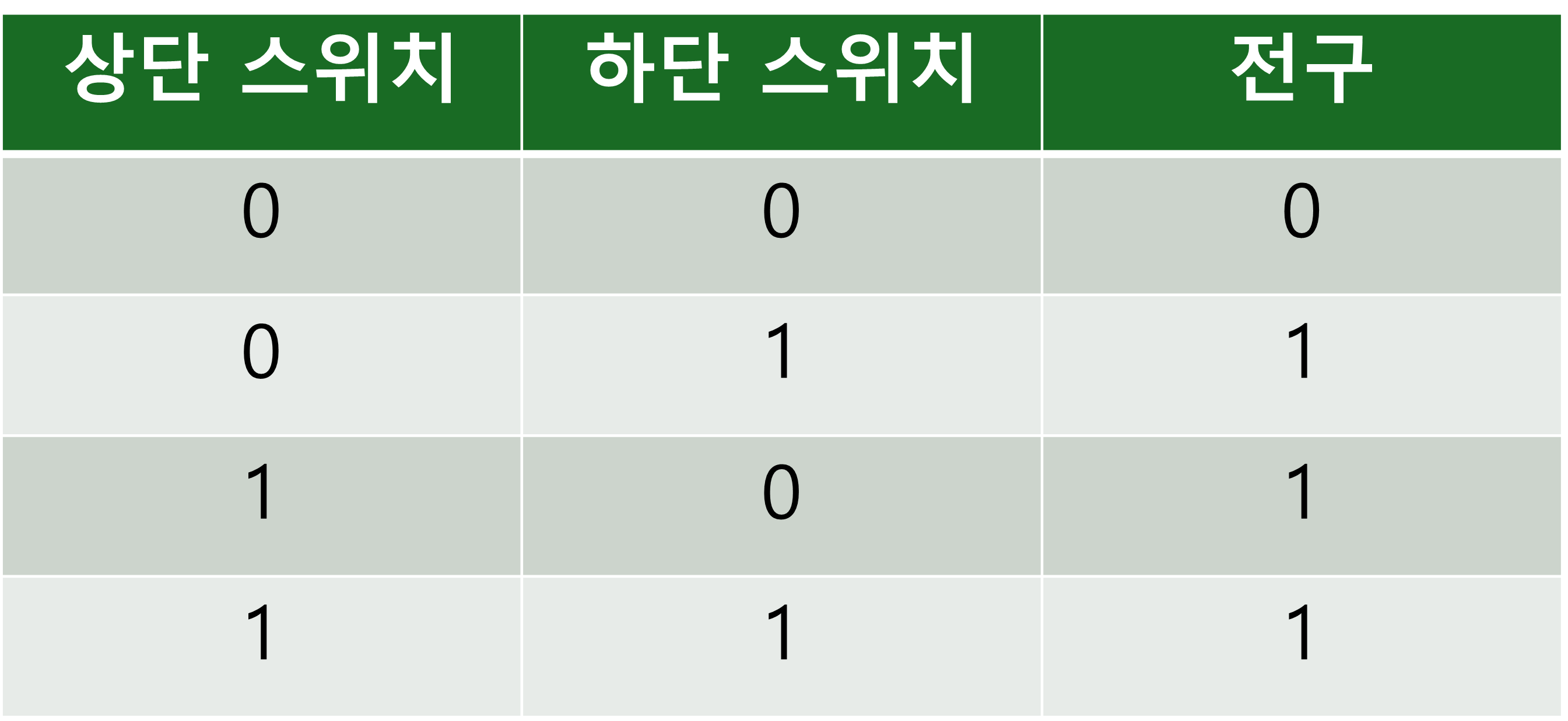
스위치의 위치를 변경해도 결과에 영향을 주지 않음을 알 수 있습니다. 즉, 스위치의 배치 순서는 중요하지 않습니다. 이는 OR 연산의 특성과 일치합니다.
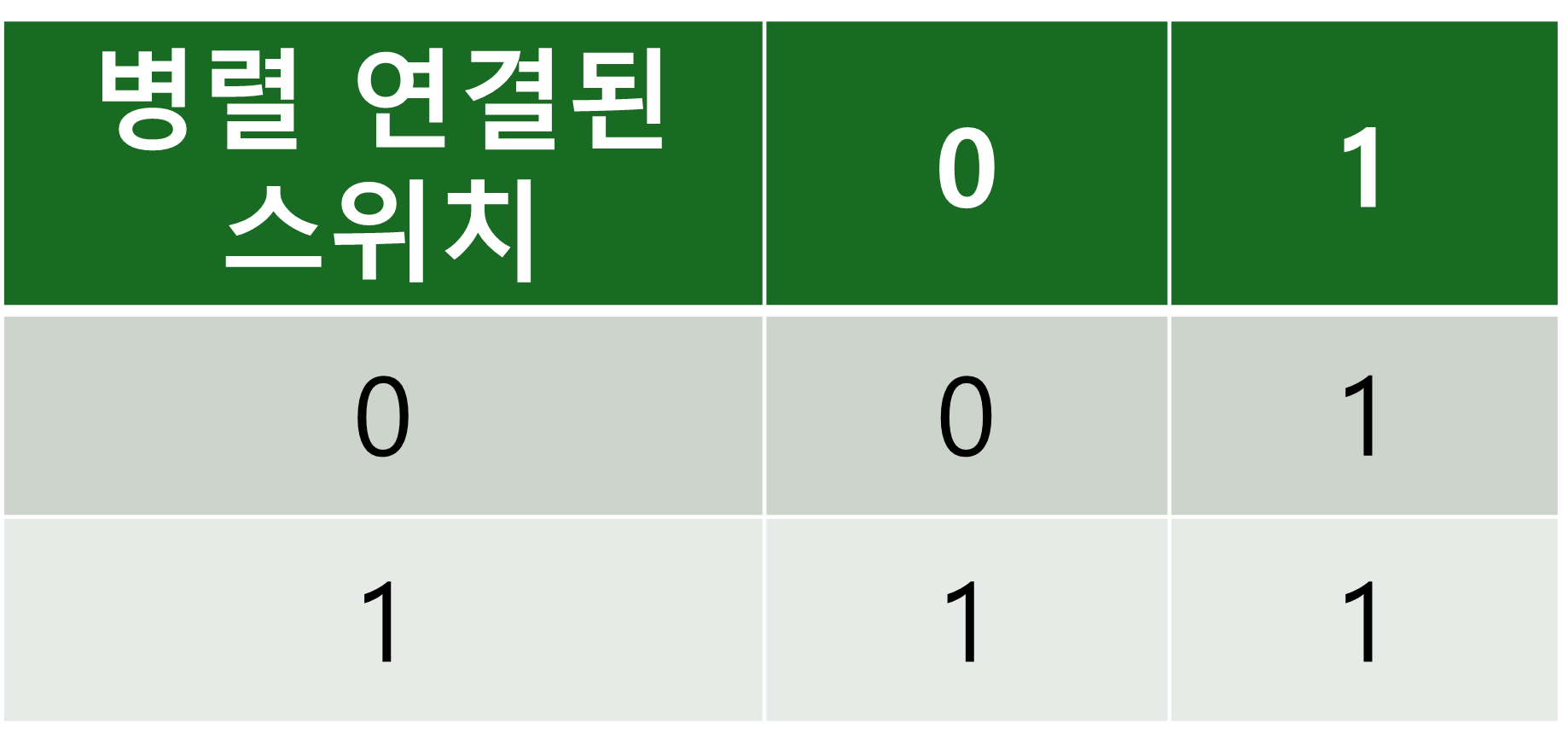
병렬로 연결된 스위치 구성은 부울 대수의 OR 연산을 실제로 시현합니다.
애완동물 가게에서의 초기 대화에서 제시된 조건을 충족하는 고양이를 찾기 위한 수식은 다음과 같았습니다.

이제 병렬과 직렬 연결의 이해를 바탕으로, 이 수식을 실제 회로에 적용하여 8개 스위치를 사용한 구성을 계획할 수 있습니다. 각 스위치는 수식의 해당 문자에 매치되며, 수식의 AND 연산은 스위치의 직렬 연결로, OR 연산은 병렬 연결로 표현됩니다.

판매원이 중성화되지 않은 수컷 황갈색 고양이를 가지고 나왔습니다. 해당되는 스위치들을 닫아 볼까요?

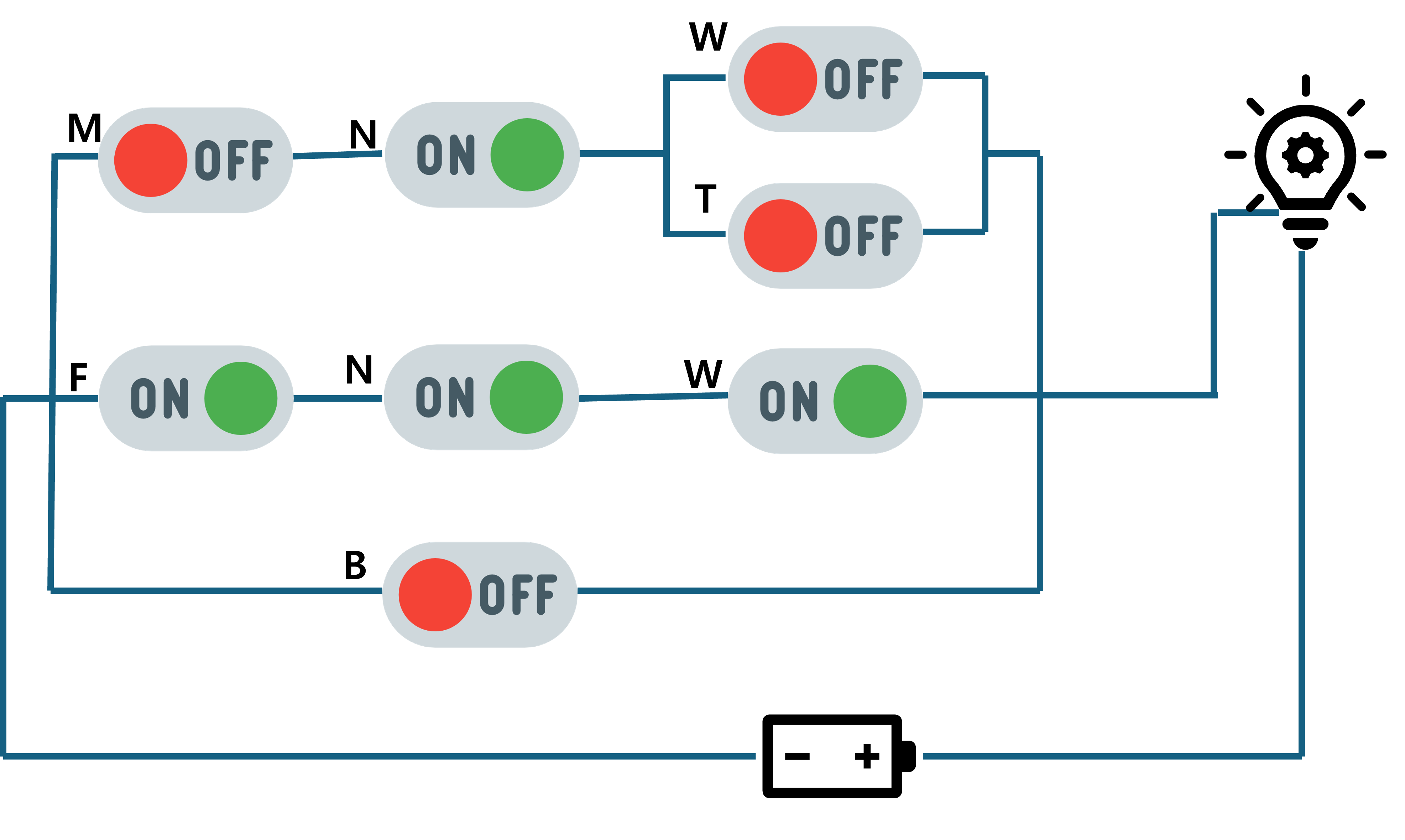
해당되는 M, T, NOT W 스위치를 닫았지만 회로의 마지막에 달려 있는 전구에 불이 들어오지는 않는군요. 그 다음으로 판매원이 가지고 온 중성화된 암컷 하얀색 고양이에 대해서도 해 볼까요.
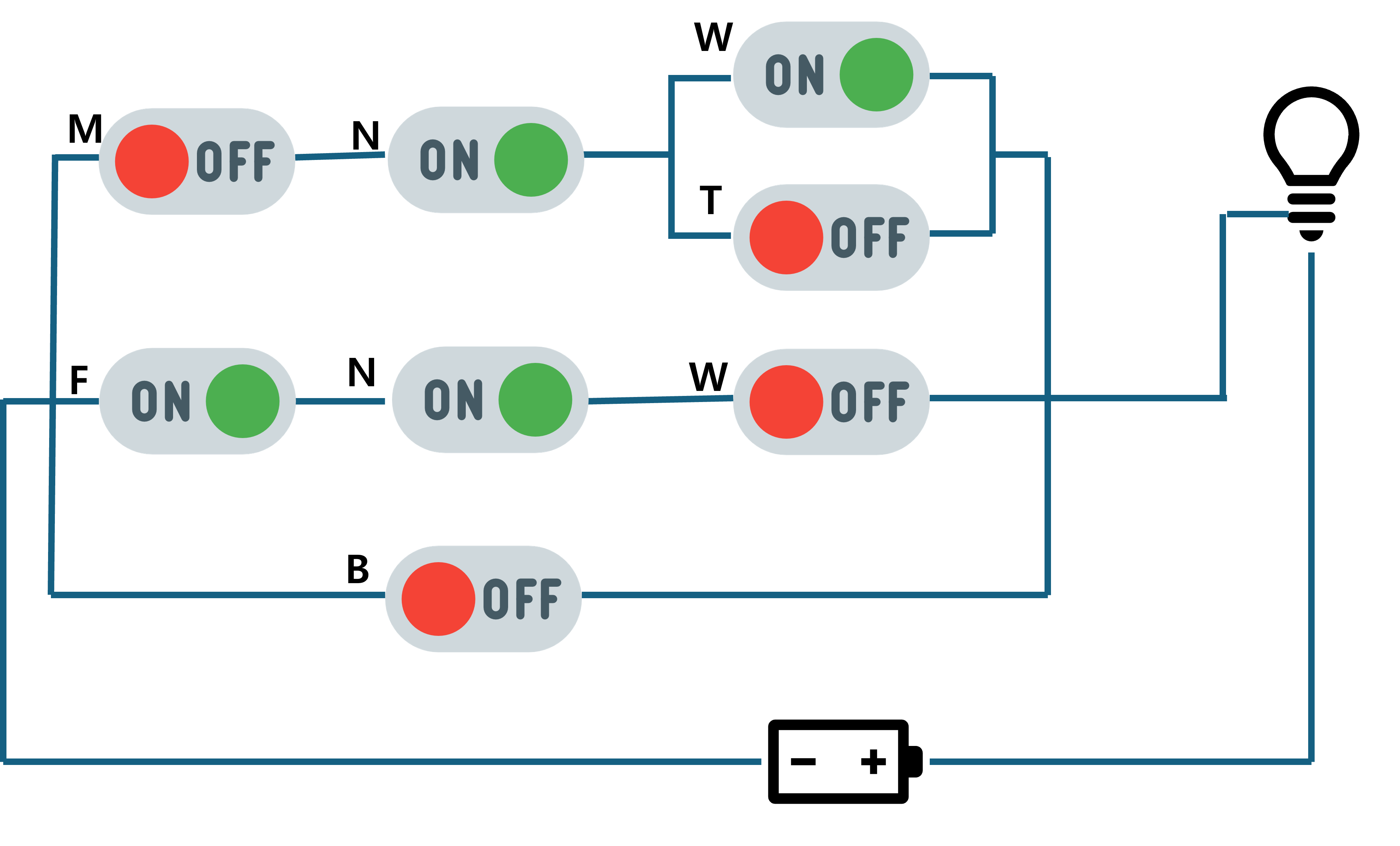
마찬가지로 오른쪽의 스위치들이 전체 회로를 닫을 수는 없었습니다. 이제 마지막으로, 판매원이 가지고 온 중성화된 암컷 회색 고양이에 대해서 해 봅시다.
조지 부울 자신이 이러한 전자 회로를 직접 구현한 적은 없으며, 그의 이론이 실제 전기 회로에 적용될 것이라고 상상조차 하지 못했을 것입니다. 부울의 시대에는 아직 백열전구가 발명되지 않았으니, 그의 이론이 후대에 전자공학의 기초가 될 것임을 예측하기 어려웠을 것입니다.
'IT 기초' 카테고리의 다른 글
| 게이트, 컴퓨터를 구성하는 기본단위(2) (0) | 2024.02.24 |
|---|---|
| 게이트, 컴퓨터를 구성하는 기본 단위 (0) | 2024.02.22 |
| 0과 1, 컴퓨터의 논리(4) (0) | 2024.02.20 |
| 0과 1, 컴퓨터의 논리(3) (0) | 2024.02.19 |
| 0과 1, 컴퓨터의 논리(2) (0) | 2024.02.16 |



